奇妙的快速傅里叶变换

2024/1/12 数学模板数学数论快速傅里叶变换 NTT FTT

快速傅里叶变换知识整理

前置知识

点值表示法

对于一个次多项式：

可以由个点确定其表达式，也就是说我们可以使用个点完整表述这个多项式。

由此我们衍生出的新的表示方法 点值表示法，使用个点来描述这个多项式。

卷积

这里我们需要了解卷积函数的一个性质：

多项式相乘

对于两个多项式和，他们的乘积为。

如果使用 系数表示法 ：我们需要枚举和的每一位系数，时间复杂度为

如果使用 点值表示法 ：

奇妙的傅里叶变化 - 多项式乘法.png

观察可知，如果两个多项式去相同的，得到不同的值，只需要将值对应相乘即可，时间复杂度为。

复数

定义：，其中。

运算规律
加法
减法
乘法
除法

幅角（相位角）：从原点出发、指向轴正半轴的射线绕原点逆时针旋转至过这个点所经过的角。

在极坐标下，复数可以使用模长和幅角来表示：。对于复数来说。
$任意$

单位圆

定义：复平面上圆心在原点且半径为的圆。

圆上点的坐标： $（）$

当将圆等分成分，可得方程的个复数根

单位根

复数相乘的重要法则：模长相乘，幅角相加（可以利用合角公式来证明）：

对于来说要求，即为的倍数，这样子可以进行二分递归。

对于来说，性质将更多的补充：

周期性：
对称性：
折半性：

对于上述的有关规律我们都可以使用欧拉定理将三角函数转换成指数形式进行计算。

离散傅里叶变化（DFT）

对于任意的多项式转点值表示，我们可以将任意个值代入计算，而时间复杂度为。

代入之后我们就可以将多项式之间的乘法变为的。

为了优化算法，伟大的傅里叶取了一些特殊的点代入进行优化。

代入 $，$ 这个点，然后求解对应的。

如果使用矩阵封装后的表示形式即为：

快速傅里叶变化（Fast Fourier Transform）

对于一个系数型多项式系数为

对于 DFT 进行点值转换的过程来说，我们希望将其加速优化。
$偶项奇项$
设：

则：

将代入得：

结合上述的分析：

的系数为
的系数为
的系数为

$，$

当时，

接下来我们进行二分递归进行计算。

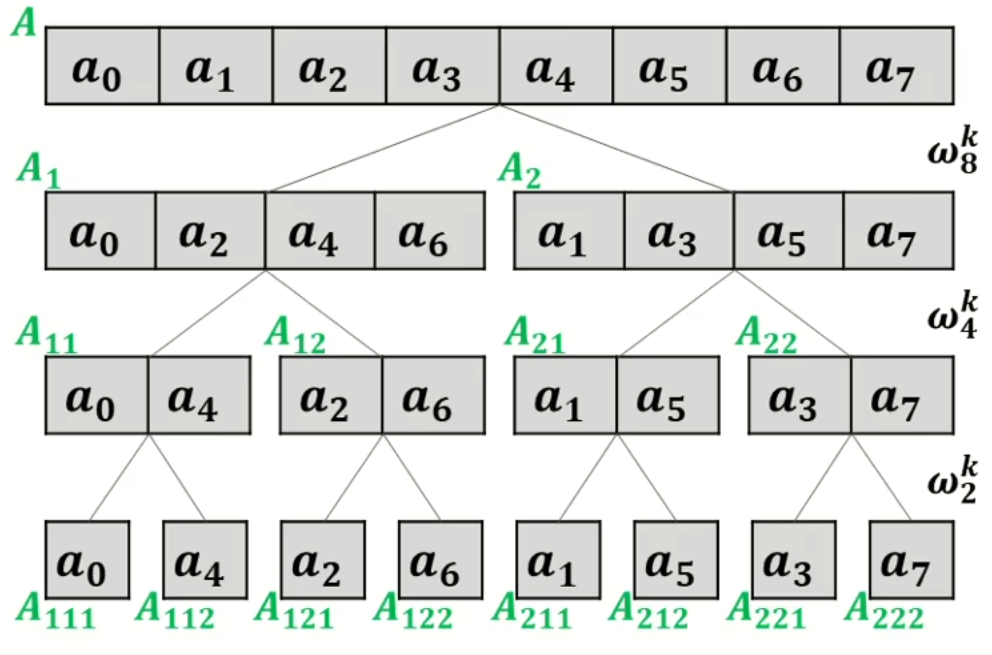
一共层，每层计算量，时间复杂度为，极大优化了 DFT，把时间复杂度降低到了可接受范围。

示例：计算。

初始化： $，，$

$，$

$，$

$，$

$，$

同理递归计算和对应表达式的值。

快速傅里叶逆变换（IFFT）

既然我们已经将两个多项式从系数表示法转换成了点值表示法进行相乘得到了最终要求的多项式的点值表示法，现在还有最后一步，就是将点值表示法转换成系数表示法，也就是进行快速傅里叶逆变换（IFFT）。

前置数学推导：

即为的共轭复数

启发点

完全方公式：

我们可以发现后一项就是的幂方和，使用等比数列求和公式可得。

则对于的个根（也就是说为次单位根）中：

只有当时，

否则当时，

快速傅里叶逆变换

设多项式

变为点值表示式：

其中

构造多项式

代入个单位根的倒数

得到点值表达式

可得：

当时，内层的和式为

当时，根据等比数列求和公式可得 内层和为

所以，即

然后再这个过程中和快速傅里叶变化（FFT）唯一不同的一点就是我们代入的是 单位根的倒数 ，也就是 单位根的共轭复数 。

所以在的基础上将改为即可

递归版本 FFT

void FFT (vector<complex<double>> &A, int n, int inv) {
    if (n == 1) return;  // 递归终点
    
    int mid = n >> 1;
    vector<complex<double>> A1(mid+1), A2(mid+1);
    
    // 奇偶分离
    for (int i = 0; i < mid; ++i) {
        A1[i] = A[i*2];
        A2[i] = A[i*2+1];
    }
    
    // 递归计算
    FFT(A1, mid, inv);
    FFT(A2, mid, inv);
    
    // 初始化
    complex<double> wk(1, 0);
    complex<double> w1(cos(2*PI/n), inv * sin(2*PI/n));
    
    // 计算对应多项式乘法
    for (int i = 0; i < mid; ++i) {
        A[i] = A1[i] + A2[i]*wk;
        A[i+mid] = A1[i] - A2[i]*wk;
        wk *= w1;
    }
}

FFT 的优化

三次变成两次

我们可以观察这个式子：

对于多项式，来说我们将放到的虚部，求出后将其虚部除以我们就可以得到了，这样子我们就只需做两次即可。

证明：

我们所需要求的为：

我们将替换成得到：

对于我们如果只取其结果的虚部为：

可以看出来其 虚部除以 得到就是的值了。

蝴蝶变换

蝴蝶变换.png

观察上述递归 起始态 和 最终态，我们可以发现他们进行了位逆序变换，我们可以利用这个特性跳过向下递归的这个过程同时节约空间利用效率。

原理简单说明：

观察我们向下二分的这个过程，每个数的二进制位上第一个位如果是那么这个数将移动到右区域，接着我们的将所有的下标右移一位，我们就可以得到连续的一组从开始的序列，这就和开始的一致了所以说我们可以通过二进制数的每一位来判断这个数接下来的位置，这样子就很好解释为什么这些数进行了一个二进制反转了，一个数的从上往下位移和这个数的二进制逆序从下往上的位移是一致的所以就出现了蝴蝶变换。

对于蝴蝶变换的过程有种有意思的优化方式使用的性质进行递推：

首先我们递推到第位的时候我们已经计算出了的反转位利用这点，我们知道相当于将这个二进制数右移了一位，这里我们相当于得到的是反转后左移了一位，所以我们右移一位还原并加上的 第一位 到的 最高位 上。

利用这个递推我们就可以在的时间内递推出 位逆序变换 了。

void change (vector<complex<double>> &A, int n) {
    vector<int> rev(n+1);
    for (int i = 0; i < n; ++i) {
        rev[i] = rev[i/2]/2 + ((i&1) ? n/2 : 0);
    }
    for (int i = 0; i < n; ++i) {
        if (i < rev[i]) swap(A[i], A[rev[i]]);
    }
}

void FFT (vector<complex<double>> &A, int n, int inv) {
    change(A, n);   // 蝴蝶变换
    for (int k = 2; k <= n; k <<= 1) {      // 层枚举
        complex<double> w1(cos(2*PI/k), inv * sin(2*PI/k));
        for (int i = 0; i < n; i += k) {    // 块枚举
            complex<double> wk(1, 0);
            int mid = k >> 1;
            for (int j = 0; j < mid; ++j) { // 块内枚举
                complex<double> x = A[i+j];
                complex<double> y = A[i+j+mid]*wk;
                A[i+j] = x+y;
                A[i+j+mid] = x-y;
                wk *= w1;
            } 
        }
    }
}

LOADING...